情報処理論 1998..2000年度 講義資料
[Index] [Prev] [Next] [References]
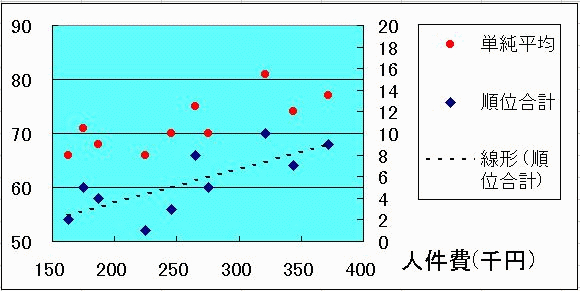
今回の人事考課試験の成績は社員の人件費と如何なる関係があるかを調べるために,まず,5科目の単純平均と順位合計(の順位)のどちらの方がより明確な関係が得られるのかを検討する。 この目的のために最も直感的で利用し易いのは散布図である。 散布図はXYグラフの一種である。 人件費をX軸に,Y軸にSheet1の単純平均(L列), Sheet2 の順位合計(K列)を指定して下図のような散布図を Sheet3 に作成しなさい。
準備として,RANK 関数による順位の計算はすべて昇順(第3引数が"1")で行われているものとする。 Sheet1 のK列に5科目の合計点,L列に5科目の平均点を計算しておく。範囲が2つの Sheets に別れているので,まず人件費に対する単純平均をグラフ化し,後から順位合計を追加する方法を説明する。


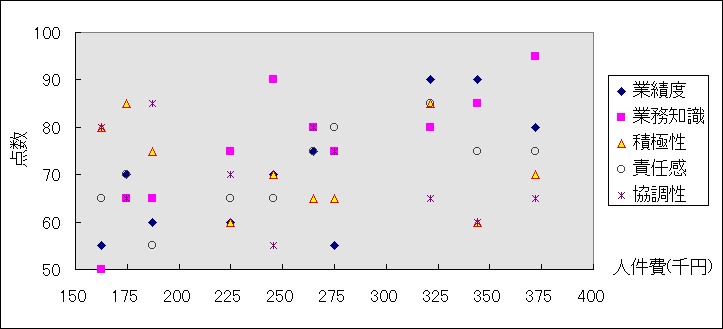
練習問題3.6: 人事考課において重要な評価科目は何か,人件費はどの科目と如何なる関係にあるのか? このような目的をもってデータ全体を概観するために,Sheet1 の人件費および5科目の点数データに関して,Sheet3 に下のような散布図を描きなさい。 このグラフでは人件費を横軸にとってあるので1人のデータがすべて縦一列に並んで表示されていることに注意する。グラフウィザードが決めた図ではマーカーの色やサイズなどが見ずらい場合は,自分で編集する必要がある。
練習8: データのグループ化と自動集計(データベース機能)
データベース機能の自動集計を使うと,特定の項目たとえば「支店」についてデータをグループ化し,他の項目たとえば科目ごとに合計や平均を計算するとか,個数を求めるとかできる。 Excelのヘルプ(トピックスを自動集計で検索)または,教科書①のp.185, 教科書②のp.52を参照して操作法を学びなさい。
各支店に勤務する社員の配置が適切かどうか見るために,支店ごとにすべての数値項目に対して平均を計算する。
次のような集計表を作成しなさい。(ここでは紙面の節約のために西区と中央区のレベルを上げてある)
まず,準備として Sheet1 のデータを他のSheetに(Sheet4とする)複写し,Sheet4
で集計したい項目である「支店」について必ず並べ替えをしておくことを忘れずに。
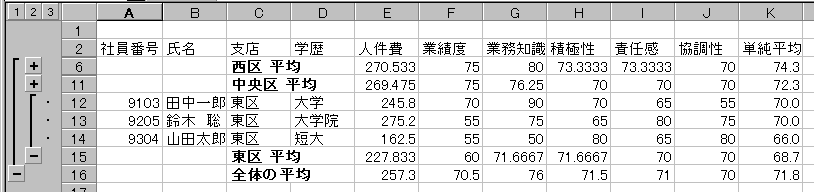
(注:図を修正した。1999/11/17)
練習9: クロス集計(データベース機能)
次の図のように,2つ以上の項目を選んで,それらの組合わせに対して,個数,合計,平均などを計算することをクロス集計という。Excelでは「ピボットテーブル」ウィザードを使って対話的にクロス集計表を作ることができる。その方法については,ヘルプ(トピックスで「ピボットテーブル」を検索し,構成を見る),教科書②のp.43~45, または参考書③p.182~185を参照しなさい。
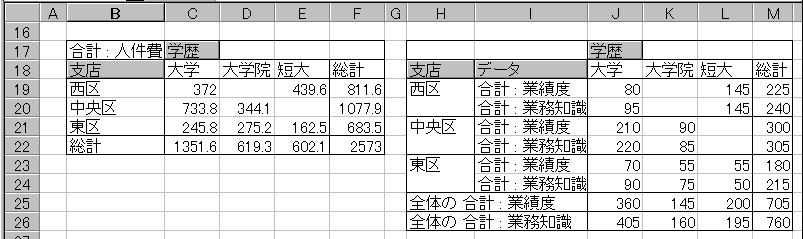
ピボットテーブルを利用して,次のような2つの集計表を作成しなさい。左の集計表は支店と学歴ごとの人件費の合計,右は同じく業績度と業務知識のそれぞれの合計を計算したものである。
例えば,この集計表からは社員の支店配置のバランスについて,東区支店は人件費が高い割には業績度も業務知識も低いことが明らかになる。(あるいは,試験の内容が不適切の可能性もある)
次の表は,最近(主に, 1993年)の情報流通供給量を中心に,情報サービス業の売上高などのデータを地域別に集計したものである。 大卒者の就職者数のうち,地域内高卒者数と卒業した大学所在地域内に就職した人数を与えてある。 地域区分は,東京圏 = (東京,千葉,神奈川,埼玉),大阪圏 = (大阪,京都,兵庫),東北 = (東北6県,新潟),関東 = (東京圏,茨城,栃木,群馬,山梨,長野),近畿 = (大阪圏,滋賀,奈良,和歌山),としてある。 下線部分に注意。北海道,東海,北陸,中国,四国,九州,沖縄については自明であろう。 以下の問に答えよ。
(1)所得水準を, 1人当りの県民所得について全国を100とした指標として定義する。これをL列に計算しなさい。 (国際的には,1$ = 107.84円換算で,スイス =$ 29903,ルクセンブルグ =$ 27094,日本 =$26919,アメリカ =$ 19462,の順に多い)
(2)表にある各項目を利用して,地域の横断面データを比較検討したり,その情報流通供給量の特徴を読み取りなさい。(加工した表またはグラフを作成するだけでなく,何がわかるかもコメントすること)
(3)北海道は情報サービス業の社会基盤があり,盛んであると言えるかどうか,これらのデータに基づいて議論しなさい。
| 年度 | 1995年 | 1993年3月卒 | 1992年 | 1993年 | 1993年 | 1993年 | 1993年 | |||
| 単位 | 1000人 | (%) | 人 | 人 | 1000人 | 億円 | 人 | 億円 | 10テラワード | 千円 |
| 大学等 | 大卒者の就職者数 | 全産業 | 情報サービス業 | 情報流通 | 1人当り | |||||
| 学生数 | 進学率 | 大学所在地 | 地元高卒者 | 就業人口 | 総生産高 | 従業員数 | 売上高 | 供給量 | 県民所得 | |
| 北海道 |
82.8
|
28.5
|
10143
|
7213
|
2850
|
184832
|
8112
|
1302
|
1510
|
2731
|
| 東北 |
136.3
|
27.7
|
17388
|
6719
|
6419
|
39083
|
19175
|
1811
|
2531
|
2547
|
| 関東 |
1134.8
|
36.2
|
156668
|
46176
|
22968
|
1833038
|
269557
|
43340
|
15058
|
3474
|
| 東海 |
217.2
|
44.1
|
29195
|
15609
|
8022
|
569834
|
30255
|
3818
|
4363
|
3125
|
| 北陸 |
51.5
|
45.9
|
5892
|
2112
|
1722
|
112044
|
5821
|
772
|
747
|
2845
|
| 近畿 |
513.9
|
43.0
|
69261
|
25419
|
10526
|
798392
|
65683
|
8955
|
5838
|
3104
|
| 中国 |
125.7
|
41.6
|
15228
|
6544
|
4071
|
272348
|
16329
|
1731
|
1867
|
2726
|
| 四国 |
48.4
|
41.1
|
6331
|
2812
|
2150
|
126006
|
7005
|
812
|
1000
|
2504
|
| 九州 |
221.4
|
36.1
|
28484
|
12936
|
6480
|
411266
|
22239
|
2454
|
2920
|
2509
|
| 沖縄 |
14.7
|
22.9
|
1311
|
950
|
548
|
31443
|
1486
|
149
|
155
|
2108
|
| 東京圏 |
1038.4
|
36.5
|
145866
|
42981
|
17562
|
1488648
|
249603
|
41091
|
11810
|
3651
|
| 大阪圏 |
447.3
|
43.1
|
64478
|
24332
|
8644
|
682972
|
63438
|
8722
|
4868
|
3201
|
| 全国 |
2546.6
|
37.6
|
339901
|
126490
|
65756
|
4730005
|
445662
|
65144
|
35989
|
3037
|
| 出所 | 北海道東北開発公庫 『地域指標ハンドブック 1996年版』 | |||||||||
|
(注)
|
テラ(tera-)は10進数桁数を表す接頭語の1つで,10の12乗の大きさ, 10テラワード = 10兆語 | |||||||||
Go to TOP
----- Last updated: