3. 統計データの読み方（Excelによる統計解析）

3. 3　統計分析ツール（２）

1. ヒストグラムツール

　【例題3】

Excelのヒストグラムツールを適用して、 上と同じ身長データに関する度数分布表やヒストグラム（度数分布を棒グラフで表したもの）を作成する。（参考書 3: 2.3.3節）

1. 度数分布表のデータ区間を表として準備する。
   ここでは、データ区間を「160以下」「160より大きく165以下」…「185より大きい」と5間隔で区分けすることにする。Excelでは、列方向に「160, 165, 170, 175, 180, 185」の6個の数値を指定する。Sheet1のセルI4に「データ区間」を、セル範囲「I5:I10」に入力する。
   • Excelでは区間の指定は、a < x <= b とする。 　
   • データ区間の数は、データの個数に対応して下表を目安に決めるとよい。 ヒストグラムツールでは、区間の幅は等間隔でなくともよい。
     

     データの個数	データ区間の数
     10 〜 25	4 〜 6
     25 〜 100	6 〜 10
     100 〜 250	7 〜 12
     250 〜	10 〜 20
     一般	データの個数の平方根

2. ヒストグラムツールを開く。

3. [ヒストグラム]ダイアログボックスで以下のように指定する。
   1. 入力範囲(I)は、$C$4:$C$29
   2. データ区間(B)は、$I$4:$I$10
   3. チェック：ラベル(L)   （先頭行をラベルとして使用する）
   4. 出力先(O)は、Sheet3!$A$1
   5. 元のデータをこの出力で上書きしてしまわないように注意する。別のワークシートを指定するのが安全である。入力ボックスをクリックしてから、Sheet3を選択し、Sheet3の左上隅の全セル選択ボタンをクリックするとこの表示（Sheet3!$A$1）が出る。
   6. チェック：累積度数分布の表示(M)
   7. チェック：グラフ作成(C)

4. ヒストグラムツールの結果と解釈
   1. Sheet3に身長データの集計結果が出力される。
   2. 一般にこのようにして得られたヒストグラムは、見やすいように編集し直したほうが良い。
   3. ヒストグラムの形状から、データの分布の状態を把握することができる。 もし、隣り合う棒グラフの高さがバラバラで、櫛の歯状になっているときは、データ区間の分け方が不適切な場合であることが多い。区間の幅と数を変更して、もう一度実行する。

5. FREQUENCY関数の使い方：(統計グループにある)

   FREQUENCY関数は２つの引数( <データ配列>, <区間配列> ) をもつ。配列とは複数データの並びを全体（セット）として１つの対象として計算できる数学的量である。 FREQUENCY関数は <区間配列> のデータを参照して <データ配列> のデータの頻度分布を計算し、結果を列方向の <頻度配列> として返す。

   【例題3】をヒストグラムツールに頼らず答えるには、まず、FREQUENCY関数を使って頻度分布表を作成する。Sheet1に元になるデータと区間データがあるものとする。

   1. 度数を出力するセル範囲 J5 : J11 を選択して、関数ウィザードを開き、統計グループからFREQUENCY関数を選ぶ。<頻度配列> のセル範囲は <区間配列> のそれより１つ多いことに注意。
   2. <データ配列> にはセル範囲 C5 : C29 を、<区間配列> にはセル範囲 I5 : I10 を指定する。データのある範囲のみを指定する。
   3. 上で〔OK〕ボタンを押すとSheet1のセル J5 に 160cm以下の頻度として"0"という答えが表示される。〔OK〕ボタンを押す前に、FREQUENCY関数のダイアログには答えとして 配列 {0, 5, 7, 8, 4, 1, 0} が表示されていたことに注意してほしい。
   4. 答えの頻度配列を求めるには、もう一度セル範囲 J5 : J11 を選択し、数式バーにはセル J5 の配列数式が入力されていることを確認してから、３つのキー [CTRL} + {Shift] + [Enter] を同時に押せばよい。

   ヒストグラムの作成：
   頻度分布表がセル範囲 J5 : J11 に得られたら、これを元に棒グラフを作成すればヒストグラムツールが与えるものと同じようなヒストグラムを作成することは容易であろう。

2. 相関ツール

２つの変数の間に直線的な関係があるとき、それら２変数の間には相関 (correlation)があるという。 ２つの変数の一方を横軸にとり、他方を縦軸にとって散布図を描いてみれば、相関のあるなしについて大凡の判定ができる。 下の図は変数 x, y のいろいろな値の組 (x, y) 10個を散布図で表したものです。
相関の有無および強さをより客観的（統計的）に判定するには、各々の図中にも示してあるように、相関係数 rなどの統計量を用いる必要がある。

相関係数と相関の強さ（大体の目安）

相関係数 ｒ の値	相関の程度
1 > | r | >= 0.8	強い相関がある
0.8 > | r | >= 0.6	相関がある
0.6 > | r | >= 0.4	弱い相関がある
0.4 > | r | > 0	殆ど相関がない

相関関数 r は次の数式（定義式のまま）で計算できます。

r = ρ_{x, y} = {[1/n] Σ_j=1ⁿ ( x_j-μ_x ) ( y_j-μ_y ) } / σ_x σ_y

ここで, n はデータ数, μ_xとμ_yはそれぞれ変数x, y の平均値，σ_xとσ_yは標準偏差です。 定義式からr の値は -1 <= r <= +1 の範囲内にあることがわかる。

図3.3-1

1. 散布図による相関の判断
   • 例題1のExcelファイルを開き，ブック名を「相関ツール」として保存する。例題1〜例題3で作成したシートは削除する。
   • ワークシートを1枚挿入し，シート名を「散布図」とする。
   • この25人分のデータに関してはかなり強い正の相関があると観察される。
2. 相関ツールの利用
   • [ツール]メニューから[分析ツール]―[データ分析]のダイアログボックス内の「相関」を選択し，[OK]をクリックする。 　
   • [相関]のダイアログボックスの入力ボックスに必要事項を入力する。 　 　

     ・入力範囲：$C$4:$D$29 ・チェック：データ方向は[列] ・チェック：先頭行をラベルとして使用 　 ・出力先：散布図!$B$23

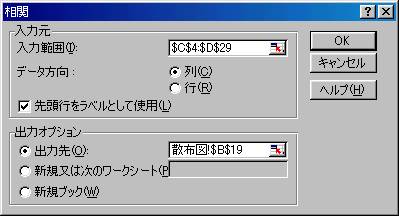     図3.3-2

     　
   • 相関係数の表と解釈

     ・シート名を「散布図と相関係数」に変更する。 　 ・相関係数の結果は r=0.83069 となっており，確かに強い正の相関があると結論付けられる。

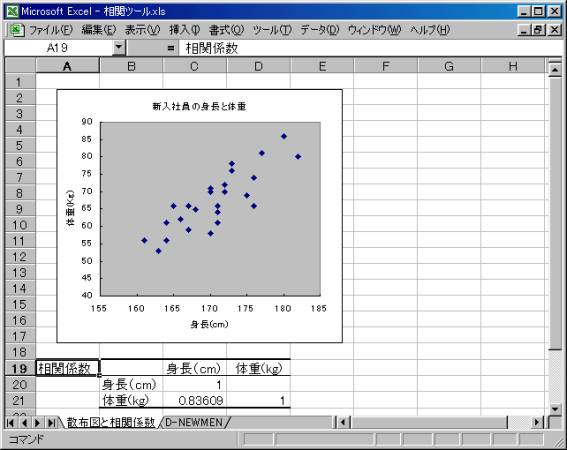     図3.3-3