練習４   基本図形を繰り返し描く

• 繰り返し処理
• 練習4a：縦横の罫線を繰り返し描く
• キャスト
• 文字列の連結
• 表示画面の座標系
• 練習4c：直線を360度回転して描く

繰り返し処理

for文（forループ）はブロック内の処理を指定した回数だけ反復処理します。

for文の書き方
for (s1; s2; s3) {
  繰り返す文;
  （for文の{ }内をforブロックまたはforループの範囲と呼ぶ）
}

• s1=初期化の式、例：int j=1;（j の初期値を 1 とする）
• s2=繰り返しの条件式、例：int j<10;（ j < 10 が不成立なら終了する）
• s3=繰り返しの増分式、例：int j=j+1;（j++; と書いても同じ。j の値を1ずつ増やす）

for文のブロックに別のfor文を含むことができます。これをforループの入れ子と呼びます。次の例では内側の文Bは 36 (=9*4) 回だけ実行されます。文Aと内側のfor文は共に 9 回実行されます。

for (int i=1; i<10; i++) {
   繰り返す文A;
   for (int j=0; j<20; j=j+5) {
      繰り返す文B;
   }
}

練習4a：縦横の罫線を繰り返し描く

練習： Appletviewerの幅と高さに合わせて等間隔に複数の横罫線と縦罫線を描いてみよう。



• Appletviewerの幅と高さを取得する

    w = getWidth();        // 幅を取得し，w に代入
    h = getHeight();       // 高さを取得し，h に代入

• キャスト
draw method（例えば drawLine ）の引数はほとんどが int 型です。 Appletviewerの幅や高さを等分割する場合、1単位の長さは整数になるとは限らず一般には実数となります。Javaで実数を扱う基本データ型は float型（32ビット長，精度は約7桁）とdouble型（64ビット長，精度は約15桁）です。整数を扱う基本データ型には int型（32ビット長）の他に、short型（16ビット長）とlong型（64ビット長）があります。
Javaでは大きなビット長のデータを小さなビット長のデータに代入することは禁止されています。このような代入を可能にするデータ変換をキャストと呼びます。


キャストの書き方
（変換したい型）式
例： int型の変数 jx に double型の式 w-ux を代入するには以下のように書く
     jx = (int)(w-ux);

• Javaのプログラム（その1）

package graphics04;

import java.awt.*;
import java.awt.event.*;
import java.applet.*;

public class GraphicsBasicsApplet4 extends Applet {

  public void paint(Graphics g) {
    double w, h, ux, uy;
    int nx=10, ny=10;     // x,y 軸の目盛数（分割数）
    w = getWidth();        // Appletviewerの幅wと高さhを取得
    h = getHeight();
    ux = w/nx; uy = h/ny;  // x,y 軸の目盛の単位
    double x,y;           // x,y 軸の目盛

// x,y 軸の罫線を描画（nx本とny本の最後は枠外で非表示）
    int i,j;
    // 横罫線(x=uxからx=w-uxまで)を縦軸方向にuy間隔でny本だけ描く
    g.setColor(Color.gray);
    for (i=1; i<=ny; i++) {
      x=1*ux;
      y=i*uy;
      g.drawLine((int)x,(int)y,(int)(w-ux), (int)y);
    }
    // 縦罫線(y=uyからy=h-uyまで)を横軸方向にux間隔でnx本だけ描く
    g.setColor(Color.blue);
    for (j=1; j<=nx; j++) {
      x=j*ux;
      y=1*uy;
      g.drawLine((int)x,(int)y, (int)x, (int)(h-uy));
    }
  }
  //アプレットのビルド
  public GraphicsBasicsApplet4() {
  }
  //アプレットの初期化
  public void init() {
  }
}

• 文字列の連結

文字列の連結演算子は"+"記号です。次の2つの文は同じ文字列を表示します。

g.drawString( "連結" + "演算子", 10, 20);
g.drawString( "連結演算子", 10, 20);

それでは以下の文をそれぞれ横罫線と縦罫線を描くforブロック内に追加して、罫線の始点に反復回数 i, j の値を表示してみます。 「""」は空白文字です。「String変数 + int変数」という式では「+」は連結演算子と解釈され int値をString値に変換してから文字列として連結されます。

      g.drawString(""+i,(int)x,(int)(y-uy/2));
      g.drawString(""+j,(int)(x-ux/2),(int)y);

• Javaのプログラム（その2）

for文のブロック内に、別のfor文を含むことができます。つまり、内側のforブロックが外側のfor文によって繰り返し処理されることになります。

縦罫線を描くfor文を、横罫線を描くfor文のブロック内にいれて考えると、上のプログラムは以下のようにかなり短くなります。

package graphics04;

import java.awt.*;
import java.awt.event.*;
import java.applet.*;

public class GraphicsBasicsApplet4b extends Applet {

  public void paint(Graphics g) {
    double w, h, ux, uy;
    int nx=10, ny=10;     // x,y 軸の目盛数（分割数）
    w = getWidth();       // Appletviewerの幅wと高さhを取得
    h = getHeight();
    ux = w/nx; uy = h/ny; // x,y 軸の目盛の単位
    double x,y;           // x,y 軸の目盛
// x,y 軸の罫線を描画（nx本とny本の最後は枠外で非表示）
    int i,j;
    // 横罫線(x=uxからx=w-uxまで)を縦軸方向にuy間隔でny本だけ描く
    // 縦罫線(y=uyからy=h-uyまで)を横軸方向にux間隔でnx本だけ描く
    for (i=1; i<=ny; i++) {
      for (j=1; j<=nx; j++) {
        x=j*ux;
        y=i*uy;
        g.setColor(Color.gray);
        g.drawLine((int)x,(int)y,(int)(w-ux), (int)y);
        g.drawString(""+i,(int)x,(int)(y-uy/2));
        g.setColor(Color.blue);
        g.drawLine((int)x,(int)y, (int)x, (int)(h-uy));
        g.drawString(""+j,(int)(x-ux/2),(int)y);
      }
    }
  //アプレットのビルド
  public GraphicsBasicsApplet4b() {
  }
  //アプレットの初期化
  public void init() {
  }
}

上のプログラムではx=w (w=nx*ux), y=h (h=ny*uy)となる次の場合の直線描画methodが実行されて、最初のものとは異なる結果が描かれる。

g.drawLine((int)w,(int)y,(int)(w-ux), (int)y);
g.drawLine((int)x,(int)h, (int)x, (int)(h-uy));

これを除外するには if 文で判定する。

if (x < w-ux) { g.drawLine((int)x,(int)y,(int)(w-ux), (int)y);}
うえのif文では、始点が終点より小さい場合に直線を描いている。また、縦軸と横軸の始点にそれぞれ i, j の値を表示する文も付け加えて、最初のプログラムと同じ結果を得るようにするプログラム（部分）は以下のようになる。

    for (i=1; i<=ny; i++) {
      for (j=1; j<=nx; j++) {
        x=j*ux;
        y=i*uy;
        g.setColor(Color.gray);
        if (x < w-ux) {
            g.drawLine((int)x,(int)y,(int)(w-ux), (int)y); }
        if (j == 1) {
            g.drawString(""+i,(int)x,(int)(y-uy/2)); }
        g.setColor(Color.blue);
        if (y < h-uy)
            g.drawLine((int)x,(int)y, (int)x, (int)(h-uy));
        if (i == 1)
            g.drawString(""+j,(int)(x-ux/2),(int)y);
      }
    }

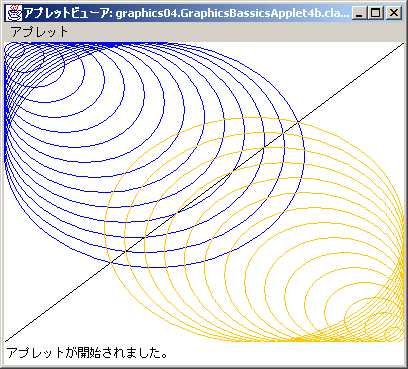
練習4b：長円を繰り返し描く

練習として，次の図のようなアプレットを作成してみよう。 右上に名前と学籍番号を書く。
描画色を決める。画面の縦横を20等分し、縦と横の1単位の大きさを決める。最小の長円から始めて画面の半分を少し超えるまで縦横の大きさを1単位ずつ大きくしながら図のような長円を描く。次に、描画色を変える。最大の長円から始めて最小の長円まで 1単位ずつ小さくしながら長円を描く。前半と後半の図形は画面の対角線（左下から右上に引いた）に関して対称（画面が正方形でないので数学的な意味では対称とは言えませんが）になるように考えてください。

2003年度の課題５
締切日   １次：12/24(Wed),   最終締切日：2004/01/20(Tue)

2004年度は課題５の一部，他は課題のページを参照のこと

表示画面の座標系

Graphicsクラスのdrawやfillで描画する点(pixel) や図形の座標系は、これまでの例題でも分かるように、数学の座標系とはかなり相違があります。多くの図形を規則的に描画するには、その違いを理解しておく必要があります。 Appletなど（JavaではAppletに限らないのですが）の表示画面の座標系はGraphics座標系とも呼ばれます。ここでは、表示画面の座標系の指定のしかたを数学の座標系と比べて説明します。



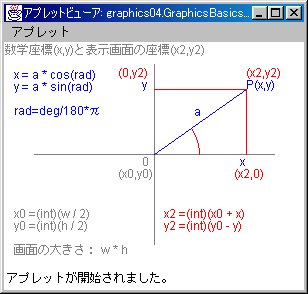
数学の座標系は、図のように、x軸とy軸の交点が座標系の原点 O (0,0) で、x軸とy軸の正方向はそれぞれ右向きと上向きです。このxy座標平面上の点Pの座標を(x,y)とします。 線分OPの長さを a とすると 三平方(Pythagoras)の定理より、 a² = x² + y² .
x軸から線分OPまでの角度を deg 度（rad ラジアン）とすると、三角比の関係式より、

x = a * cos ( rad ) ,     rad = deg /180 * π ,
y = a * sin ( rad )


表示画面の座標系(Graphics座標系)は画面の左上端が座標系の原点 (0,0) になっています。画面上の座標を (X,Y) としますと、X軸の正方向は右向きですが、Y軸の正方向は下向きです。 コンピュータグラフィックス(CG)では、最初に数学の座標系で図形を仮想的に描画し、それをGraphics座標系に変換し、実際に画面に描画文を記述します。

横幅 w，縦長 h の大きさ（単位はpixel）の表示画面では、通常のように、表示画面の中心 (x0,y0) に数学の座標系の原点 (0,0) を合わせて考えることにします。数学の座標系における図形上の点P (x,y) に対応するGraphics座標を (x2,y2) とします。このとき数学の座標からGraphics座標への変換式は次のようになります。（y座標の符号に注意）

原点 :	x0 = (int) w / 2 ,	y0 = (int) h /2
点P :	x2 = x0 + (int) x ,	y2 = y0 - (int) y

Graphics座標の単位はpixelなので座標(X,Y)の値は正の整数のみが許されます。図形の座標が表示画面の範囲からはみ出す（負の整数値や画面の大きさを超える整数値となる）場合は、その座標に対応する図形の部分が描画されないので注意が必要です。 Javaの数学関数は Math クラスの method として提供されています。高校で習う主な数学関数のmethodは以下のように書きますが、引数の型は大部分が double のみです。

method		引数x,yの型	機能
sqrt ( x )		double	実数xの平方根 √x を与える
sin ( x )		double	実数x（角度はradian単位）の正弦 sin(x) を与える
cos ( x )		double	実数x（角度はradian単位）の余弦 cos(x) を与える
exp ( x )		double	実数xの指数関数 exp(x) を与える
max (x,y),   min (x,y)		int, long, float, double	引数x,yの中から最大値または最小値を与える
random ( )		なし	実数0.0と1.0の間の乱数 ( y は0.0以上、y < 1.0 ) を与える

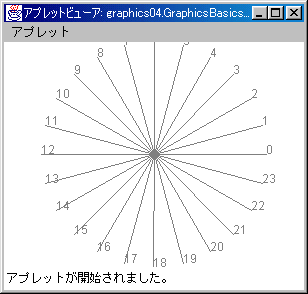
練習4c：直線を360度回転して描く

練習4c： Appletviewerの画面の中心に直線の左端を固定して、右端を15度間隔で0度から360度まで回転して24本の直線を描いてみよう。直線の長さは画面の縦横の長さの小さい方の約半分とする。


上の課題について次のような条件を加えてプログラムを作成します。
• 画面の幅を w , 高さを h とする
• 長さの小さい方を得るには Math.min (a, b) を使う
• 直線の先端に回転角またはそのに対応する文字列を書く


package package graphics04;

import java.awt.*;
import java.awt.event.*;
import java.applet.*;

public class GraphicsBasicsApplet4c extends Applet {

  public void paint(Graphics g) {
    double w, h, ux, uy, x0,y0;
    w = getWidth();       // Appletviewerの幅wと高さhを取得
    h = getHeight();
    x0 = w/2; y0 = h/2;   // 画面の中心、xy座標の原点
    double x,y,rl;        // 直線の右端のx,y座標、直線の長さrl
    rl = Math.min(x0,y0); // x0,y0の小さい方を直線の長さとする
    double rad;           // radian
// 角度degを0度から360度まで15度ずつ増やし、直線描画を繰り返す
    for (int deg=0; deg<360; deg+=15) {
      g.setColor(Color.gray);
      rad = deg/180.0 * Math.PI;
      x = rl * Math.cos(rad);
      y = rl * Math.sin(rad);
      g.drawLine((int)x0,(int)y0,(int)(x0+x),(int)(y0-y));
      g.drawString(""+deg/15,(int)(x0+x),(int)(y0-y));
    }
  }
  //アプレットのビルド
  public GraphicsBasicsApplet4c() {
  }
  //アプレットの初期化
  public void init() {
  }
}