Excel95から最適化分析ツールとして「ソルバー」機能がアドインされた。ソルバーは複数の変数を持つ問題に対する最適解を求めるもので，線形計画のみならず，最近話題の経済学的複雑系などの非線形計画問題をも扱うことができる。このソルバーを用いて，輸送計画のコストを最小にする問題(線形計画法)を解くための方法を説明する。
 

［練習問題３］ ソルバーの準備

　新しいシートを新規に挿入し、［ソルバー］と名前をつけなさい。表１と表２を［ソルバー］にコピーする（[A1:F18]）。
ここでは［ソルバー］の２つの表をまとめて表７と呼ぶことにする。表７の各桝目には輸送計画を決めるのに必要な式や値が入力されている。
　この問題にソルバーを適用するとき，まず総輸送費の式

(1) 桝目F18
は，目的セルまたは目的関数(Object function)と呼ばれる。この目的関数の値を最小にするために，セル範囲B14〜D15の数値を変化（これらを決定変数"Decision variables"と呼ぶ）させる訳である。そのとき以下の11個の制約条件：

(2) すべての決定変数は０または正，つまり
B14≧0 , C14≧0 , D14≧0 ,B15≧0 , C15≧0 , D15≧0。

(3)各小売店の残存需要量は０，つまり
B17＝0 , C17＝0 ,　D17＝0。

(4) 各作業所の残存供給量は０または正，
F14≧0 , F15≧0

を満たしながら，ソルバーは最適解を探し出す。
 
 

図１「ソルバーパラメータ設定ダイアログ」(制約条件C17 = 0まで設定したところ)

 

［練習問題４］ソルバーの実行

〔ツール(T)〕→〔ソルバー(V)〕を選択する。すると，図３の「ソルバー・パラメータ決定」ダイアログが開く。もしこのダイアログが白紙状態でなければ、〔リセット(R)〕ボタンを押す。
図１の〔目的セル(E)〕の欄にセルF18を選ぶ (表示は $F$18 となる)。その下にある〔目標値〕では，○最小値(N)のラジオボタンを選ぶ。
〔変化させるセル(B)〕の欄には，決定変数があるセル範囲B14〜D15を選択する (表示は $B$14:$D$15 となる)
「制約条件(U)」を設定するために，〔追加(A)〕ボタンを押す。すると，図２の「制約条件の追加」ダイアログが開く。
小売店Y1の列について詳しく説明する。制約条件の追加の順は問題ではないが，条件が多いので営業所の順番に追加していこう。
まず，〔セル参照(R)〕欄にセルB14を選ぶ。真ん中の比較記号欄から ≧ を選び，〔制約条件(C)〕欄には数 ０ を直接記入する。これで「B14≧0」という条件を追加したことになる。

図２「制約条件の追加」ダイアログ　(制約条件　B14 ≧0 を設定しているところ)

 

次に，〔追加(A)〕ボタンを押し，同様に，制約条件(2)　B15 ≧0, B16 ≧0 と 制約条件(3)　B17 ＝0 を設定していく。ここまでが小売店Y1に対する制約条件の設定である。
同様に，小売店Y2、小売店Y3についても制約条件(2)と(3)を設定していく。残存供給量の列に対しては制約条件(4)を設定する。ただし，最後の条件，F16 ≧ 0 ，を記入したら，〔追加(A)〕ではなく〔OK〕ボタンを押す。
すると，図１の「ソルバー: パラメータ決定」ダイアログに戻る。ここで変更や削除ができるので，ここまでの途中で間違えた場合でも〔OK〕ボタンを押して修正してから，追加してもよい。
パラメータ設定がすべて済んだら，図１で〔実行(S)〕ボタンを押す。すると，ソルバーによる計算が開始される。しばらくしてから，図３の「ソルバー: 検索結果」ダイアログが開く。

図３の「ソルバー: 検索結果」

図４「ソルバー検索結果」ダイアログ(レポートを選んでいる)

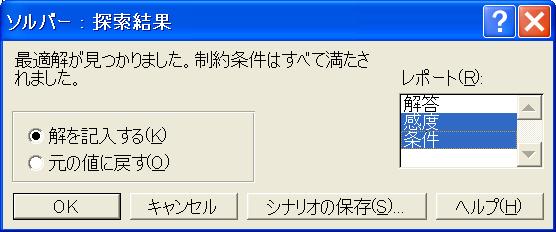
ここで，「○解を記入する(K)」を選ぶ。また，〔レポート(R)〕の欄から「条件」などを選んでみてもよい。そして〔OK〕ボタンを押す。
すると，Sheet[ソルバー]のセル範囲B14〜D15に最適解としての輸送計画の解が記入され，そのときの総輸送費1040万円がセルF18に表示される。これは確かに[練習問題２]よりも更に少ない輸送費である。
　図４で，〔レポート(Ｒ)〕の欄から「条件」や「感度」を選んだときは，それぞれ「感度レポート１」や「条件レポート１」というシート名のワークシートが挿入されて，そこに次のような解の詳細な情報が与えられる。一般に，最適解で与えられる変化させるセルの値(決定係数)は誤差を含んでいる。条件レポートはその誤差の程度を報告してくれる。感度レポートは，目的関数の係数，利用可能な資源，および技術係数(今の例では，供給可能数や需要数，および各区間の輸送単価)が変動したとき，最適解はどのように変わるかを報告するものである。
 

表１　条件レポート (「輸送問題」の最適な解は「値」欄に表示されている)

 
　条件レポート (「輸送問題」の最適な解は「値」欄に表示されている)

Microsoft Excel 7.0 条件レポート ←この標題は，Exccel97の場合，"Excel 8.0"と表示される Microsoft Excel 10.0 条件レポート          ワークシート名 : [transport.xls]条件レポート 1          レポート作成日 : 2003/12/17 11:30:27                      目的セル         セル 名前 値        $F$18 総輸送費用   1040                   変化させるセル   下 目的セル  上 目的セル  セル 名前 値  条件 値  条件 値  $B$14 X1 Y1 10.00001775  10.00001775 1040  10.00001775 1040  $C$14 X1 Y2 19.99998225  19.99998225 1040  19.99998225 1040  $D$14 X1 Y3 70  70 1040  70 1040  $B$15 X2 Y1 39.99998225  39.99998225 1040  39.99998225 1040  $C$15 X2 Y2 40.00001775  40.00001775 1040  40.00001775 1040  $D$15 X2 Y3 0  0 1040  0 1040

(※注１)最適解が複数個存在する場合がある。このときは、[B14:D15]に適当な初期値を入れておくと、別の最適解を得ることが出来る。

(※注２)最適解としての[B14:D15]の値が、整数ではなく「小数点付」で求まった場合には、その「小数点付き数値に最も近い整数値」を選択すると最適整数解が求まることが多い。
 

  線形計画法の詳しい説明は，経営科学やＯＲ(オペレーションズ・リサーチ)の入門書を参照されたい。
　なお，変数が２つの線形計画法の問題は，高校の数学「連立一次不等式のグラフ解法」でも扱われており，これをExcelのワークシート上で解いていく方法もある。(参考書?：平田純一ほか著，第6章の6.6節)
　また，線形計画問題に対するより本格的な解法として，シンプレックス法と呼ばれる数値解法を簡単な連立一次方程式の問題として解くこともできる。（教科書?：13章　ORへの応用)